

Equivalent Focal Length
What is the equivalent focal length?
As the technology has advanced, digital cameras with their digital image sensors have largely replaced traditional 35mm film cameras. This in turn has made the field of view an important optical specification to consider when selecting a camera lens. The field of view is closely related to focal length and image sensor size, but because digital image sensors do not conform to a single size standard as did 35mm film, focal length and field of view no longer possess a uniform relation. In order to redefine the relation between focal length and field of view, the photographic term "equivalent focal length" was created.
When it first appeared, the term "equivalent focal length" was defined as "35mm equivalent focal length", which means "a focal length that provides the same field of view on a 35mm film camera". Current mainstream optical sensors come in several formats, including--from largest to smallest--full-frame (FF, 36mm x 24mm), APS-H (28.1mm x 18.7mm), APS-C (23.5 x 15.6mm), and Micro Four Thirds (M4/3, 17mm x 13mm). We can illustrate the use of equivalent focal length as applied to such formats with an example. If a camera lens with a 50mm focal length is used on a camera with an APS-C (Canon) sensor, the field of view is about 30°, but if that same camera lens is installed on a camera with an FF sensor, the field of view expands to around 45°. If you wish to obtain a field of view of roughly 30° on a camera with an FF sensor, you need to use an 80mm lens. That is the equivalent of saying that the 50mm lens on a camera with an APS-C sensor has an equivalent focal length of 80mm with an FF sensor.

Figure 1. Relation between sensor formats and field of view

Figure 2. Relation between field of view and sensor/lens combinations
Why use equivalent focal length?
Due to the varying dimensions of image sensors, cameras used for surveillance applications generate a correspondingly large range of image sizes. Lenses with an identical focal length of 3mm, for example, will produce different fields of view and magnification ratios depending on the particular image sensor they are paired with. This results in confusion among customers when making purchase decisions, since a given focal length does not guarantee a particular image size. In order to resolve this difficulty, we have adopted the equivalent focal length concept, increasing the ease and intuitiveness of selecting the best option.
How to calculate the equivalent focal length
HFOV = 120°(W) ~ 46°(T)
Using our 65 Series cameras as an example, the lens used has a focal length of 4-9mm and is paired with a 1/2" image sensor. The actual measured horizontal field of view is 120° (for the wide-angle end of the lens' focal length range) and 46° (for the telephoto end). For example, if you want to know the focal length of a lens that would produce the same field of view on a camera with a 1/3" image sensor--this is the information that the equivalent focal length provides.
The ratio of the sensor diagonal dimension is about 1.5 between 1/3” sensor and 1/2” sensor. So the equivalent focal length for the wide angle end is about 2.7mm. Also consider the distortion effect, where the zoom ratio from the wide angle end to the telephoto end is about 4, so the equivalent focal length for the telephoto end is about 12mm. Therefore, we can deduce the equivalent focal length for the 65 Series cameras with a 1/3” sensor is 2.7mm ~ 10.8mm.
Table 1. Equivalent Focal Length Example
Product Model |
FD9365 Series |
|---|---|
FOV |
120° ~ 46° |
@1/2” sensor (physical) |
4 ~ 9 mm |
@1/2.7” sensor (equivalent) |
3 ~ 12 mm |
@1/2.8” sensor (equivalent) |
2.8 ~ 11.4 mm |
@1/3” sensor (equivalent) |
2.7 ~ 10.8 mm |
Supplement: Explanation of basic terms
- Sensor Size
- Focal Length
- Field of View (FOV)
- Distortion
- Zoom Ratio
As the name implies, sensor size is the size of a sensor's effective image area, and is expressed in inches, though confusingly this does not refer to the actual size of the sensor. In any case, a 1" sensor size provides an effective image area measuring 12.8mm in width, 9.6mm in height, and 16mm diagonally. When describing actual lens and sensor specifications, "sensor size" is more relevant to the matching of components rather than to actual sizes.
When we use a camera to take a photograph of an object, after light reflected by the object is collected by the lens, it is focused on the focal plane, which is the location where the image sensor is positioned. If the distance to the photographed object approaches infinity, the distance between the focal plane and the lens' "reference point" is the focal length. Because a typical optical lens is built from multiple lenses or even multiple lens modules, its structure is rather complex. To simplify the discussion, consider a single convex lens whose reference point will be the center of the lens. The focal length will then be the distance from the focal plane to the center of the lens.
"Field of view" refers to the angular extent of a given scene that a camera's image sensor can capture. Field of view is further divided into diagonal field of view (ӨD), horizontal field of view (ӨH), and vertical field of view (ӨV). Using the lens' focal length and the sensor size, we can easily calculate the theoretical size of the field of view.
Distortion is a measure of image aberration produced by a camera lens. Based on whether the calculated value is positive or negative, distortion is classified as pincushion distortion (when positive) or barrel distortion (when negative). In optical systems, distortion will give rise to a discrepancy between the actual measured field of view and theoretical field of view. Barrel distortion causes the system's actual field of view to be larger than the calculated value, while pincushion distortion results in the system's actual field of view being smaller than the calculated value.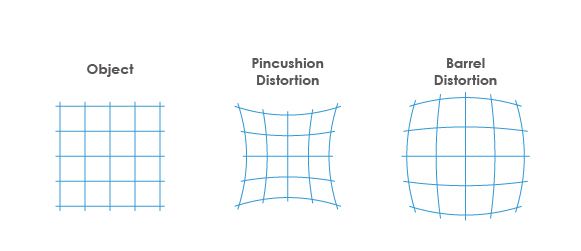
Depending on a particular application in which an optical component is used, the manner of calculating distortion may also differ. For cameras, the most common calculation methods are SMIA-Distortion and TV-Distortion, with SMIA-Distortion resulting in values twice as large as TV-Distortion.
The zoom ratio is an important specification of a zoom lens. It is defined as the amount of magnification produced in the image of an object when photographed using the telephoto end of the zoom range when compared to the image when photographed using the wide angle end--specifically, the ratio in the image heights. The figure below uses a camera lens with a focal length of 2.8-12mm to illustrate. A simple calculation yields the image height ratio, which is proportional to the ratio of the corresponding focal lengths.